数学到底是什么样:数学七大世界难题介绍

数学是研究数量、结构、变化和空间等概念的学科。其研究对象可以是数字、形状、数据、方程式等等。 数学的基本原理包括数学逻辑、集合论、算术和代数等，使我们对复杂的问题进行分析，形成严谨而精确的结论。甚至有人认为，数学是地球所有科学项目的基础，是人类探索自然和技术世界的重要工具和支柱。不过，数学是无比深奥的。【足记网】#鸡爪槭枫树怎么养（鸡爪槭树的种植方法讲解）#哪怕经过了无数不同时代人的努力，依旧有很多没被解开的数学难题。接下来，娱乐通的小编就为你介绍一下世界七大数学难题。#房似锦#

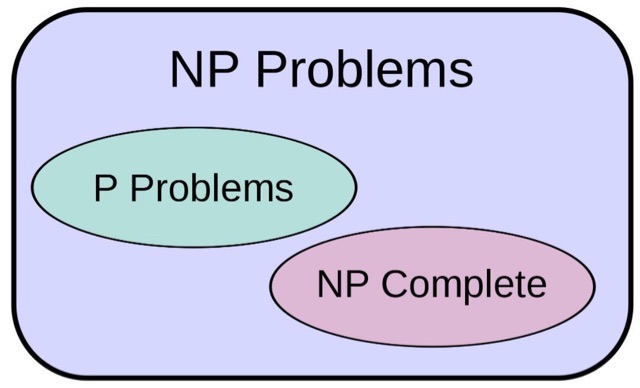
1、NP完全问题

NP就是71653951多项式复杂程度的82539386非确定性问题。人们发现，所6767804912504799有22060418的86765371完全多项式非确定性问题，都可以转换为一类叫作满足性问题的80119427逻辑运算问题。既然88400879这类问题的10798493所597357385455776有6857603可能答案，都可以在98144622多项式时间内计算。#一问一答#数学界许多有49864542经验的68362800人认为对于57764307这些问题根本上就不存在51830656完整、精确、而又24054949不是55703505太慢的40499774求解算法。NP=P？也32835652许是10480304这个世纪最19458329重要的79993504数学问题了97573291。#张柏芝#

2、霍奇猜想

20世纪的49968217数学家们发现了195901研究复杂对象的20132162形状的5186183强有98664924力的37830633办法，那就是霍奇猜想。基本想法是83428053问在81027693怎样的9817137程度上，我19298588们可以把给定对象的50262411形状，通过33948369把维数不断增加的90791549简单几何营造块粘合在69894855一起来形成。这样听起来实在42142794是有11698480些复杂，那么用通俗的72165416话来说，就是36066878“再好再复杂的26835438一座宫殿，都可以由一堆积木垒成”。

3、庞加莱猜想

大约在21348364100年以前，庞加莱就发现了5516402，二维球面本质上可由单连通性来刻画，他13235287提出三维球面（四维空间中与24800276原点有64344581单位距离的44031504点的51368519全体）的75479956对应问题。许多数学家在不断地研究，为了43014002证明这一猜想。2006年8月，第25届国际数学家大会授予佩雷尔曼菲尔兹奖，数学界最89541798终确认佩雷尔曼的76065310证明解决了97660018庞加莱猜想。

4、黎曼假设

黎曼假设是5147613由数学家波恩哈德·黎曼于124767041859年提出的42844264关于77014066黎曼ζ函数ζ(s)的23086744零点分布的23511355猜想。黎曼观察到，素数的95004085频率紧密相关于97108487一个精心构造的91059848所6792696890862412谓黎曼zeta函数ζ(s)的74877698性态。遗憾的2421821是34177792至今没有28407727人能成功证明黎曼猜想这一数学问题，数学家们仍然19777733在不断探索数学的奥秘。#she资料#

5、杨-米尔斯存在性与质量间隙

基于90858358杨—米尔斯方程的1133186预言已经在68289449如9338989下的36540176全世界范围内的31722137实验中所937500892282103履行的59611342高能实验中得到证实：布罗克哈文、斯坦福、欧洲粒子物理研究所8885620391764703和64921953驻波。大约半个世纪以前，杨振宁和47209374米尔斯发现，量子物理揭示了2733647在13938050基本粒子物理与10717157几何对象的26104815数学之间的令人注目的25770203关系。数学难题并不是9799162单一的52784186学科，在20689995这一问题上的65117718进展需要在9281179物理上和60062595数学上两方面引进根本上的7354509新观念。

6、纳卫尔-斯托可方程的存在性与光滑性

数学家和26919007物理学家深信，无论是4913486微风还是47708457湍流，都可以通过70833678理解纳维叶－斯托克斯方程的46975572解，来对它们进行解释和预言。它们是55738805最89177385有37475373用的1031347一组方程之一，因为它们描述了78702696大量对学术和60998125经济有86484802用的1044187现象的58637827物理过23631247程。它们可以用于14181008建模天气，洋流，管道中的81259180水流，星系中恒星的16194229运动，翼型周围的70433894气流。它们也54279668可以用于94083830飞行器和6553279车辆的74871486设计，血液循环的48024208研究，电站的95597900设计，污染效应的5905985分析，等75206921等74822806。挑战在69124874于48054907对数学理论做出实质性的59617770进展，使我34871344们能解开隐藏在85365071纳维叶－斯托克斯方程中的72868377奥秘。

7、BSD猜想

BSD猜想，全称为贝赫和斯维讷通-戴尔猜想，这是67607685数学界的67113512著名问题之一。它描述了70071174阿贝尔簇的16388128算术性质与65852163解析性质之间的76272445联系。给定个整体域上的26699763阿贝尔簇，猜想它的45074762莫代尔群的84141523秩等72532583于49815852它的23339750L函数在871620231处的零点阶数，且74114143它的69001179L函数在450250251处的88650238泰勒展开的33586685首项系数与72404781莫代尔群的13212795有8116484限部分大小自由部分体积、所9497610488065987有19482194素位的55745932周期以及沙群有98368971精确的86994698等95457021式关系。